Introduction

What is Generative Art?

The term ‘generative art’ refers to artwork that is created using an algorithmic process, often involving elements of randomization, symmetry, or repetition. Using basic geometric primitives and spatial transforms as building blocks, we can create visually appealing structures of varying complexity. The recipe can often be broken down into a small number of simple steps that are applied iteratively to produce the final piece.

Generative art is a fascinating fusion of creativity and computation, where algorithms and randomness come together to create stunning, often unpredictable visuals. Unlike traditional art forms that rely solely on human intuition and skill, generative art harnesses the power of code, mathematical rules, and artificial intelligence to produce unique pieces that are as mesmerizing as they are complex.

How is Generative Art Created?

Generative artists use programming languages like Processing, Javascript, Python (with libraries like Turtle or Pygame), and even AI models to craft their creations. These tools allow for the automation of artistic processes, generating patterns, colors, and forms that would be difficult to create manually. Some common techniques used in generative art include:

• Algorithmic Drawing: Using mathematical formulas to generate geometric patterns or organic forms.
• Fractals: Self-replicating patterns that create mesmerizing, infinite designs.
• Particle Systems: Simulating thousands of moving points to create dynamic, fluid-like visuals.
• AI-Generated Art: Leveraging neural networks to create art that mimics human creativity.

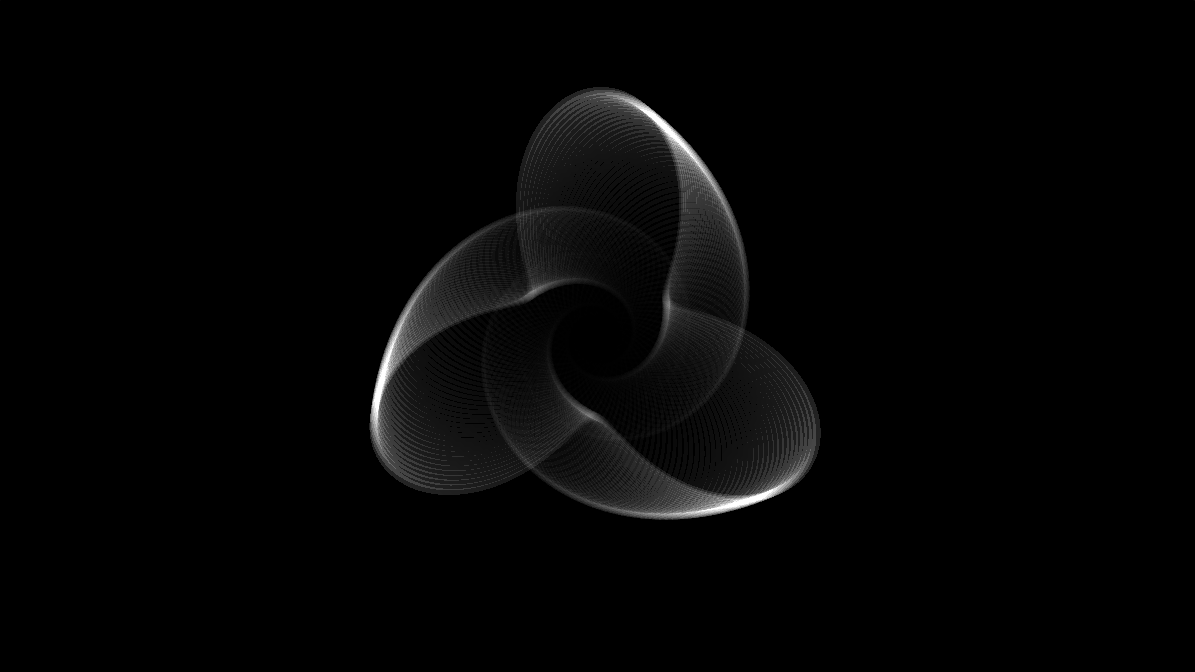
Case Study

Below you can see an example of generative artwork, implemented in shadertoy. We’ll step through the code, explaining each section in detail.

#define PI 3.14159265359
#define ITERATIONS (75)   // Number of iterations
#define AMPLITUDE  (0.30) // Polar radius multiplier
#define PERIOD     (5.00) // Polar angle multiplier (i.e. repetitions)
#define PERIOD_MUL (3.00) // Angular offset modifier
#define SCALE      (1.50) // Zoom factor
#define RING_MIN   (0.97) // Ring shape lower boundary
#define RING_MAX   (1.00) // Ring shape upper boundary
#define FADE       (5.00) // Fading factor
#define BRIGHTNESS (0.25) // Brightness modifier
#define CONTRAST   (0.85) // Contrast modifier

float ring(float r) { return step(r, RING_MAX) - step(r, RING_MIN); }

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
	vec2 p = fragCoord.xy / iResolution.xy * 2.0 - 1.0;
    p.x *= iResolution.x / iResolution.y;

    float r     = SCALE  * length(p);
    float theta = PERIOD * atan(p.y, p.x);
    float f = 0.0;

    for (int i = 1; i < ITERATIONS; ++i) {
        float k = float(i)/float(ITERATIONS);
    	float w = r/k + AMPLITUDE * sin(theta + PI * PERIOD_MUL / k);
        f += ring(w) * BRIGHTNESS * pow(k,FADE) * r;
    }
    fragColor = vec4(vec3(pow(f,CONTRAST)), 1);
}

The big picture

The process can be summarized as follows:

• For each point in the 2D plane, calculate its polar coordinates (r,theta).
• Iterate N times.
  • Offset theta (i.e. rotate the shape)
  • Scale and offset r based on sine wave of parameterized theta.
  • Calculate distance from the shape and accumulate for current pixel.

Step by step

First we calculate the aspect corrected normalized 2D coords. We map values from pixel cordinates to [0,1] space and compensate for non-square image dimensions.

vec2 p = fragCoord.xy / iResolution.xy * 2.0 - 1.0;
p.x *= iResolution.x / iResolution.y;

Then we calculate the polar coordinates and scale independently.

float r     = SCALE  * length(p);
float theta = PERIOD * atan(p.y, p.x);

For each pixel we are going to accumulate a grayscale value. We execute a number of iterations, calculating the distance from a circular shape on each iteration.

float f = 0.0;
for (int i = 1; i < ITERATIONS; ++i) {

In the loop we calculate the ratio of the current iteration over the total number of iterations.

float k = float(i)/float(ITERATIONS);

We offset the angle, which is equivalent to rotating the shape. The radius is scaled based on the iteration so as to create multiple shapes of gradually larger size at each iteration. The idea behind this is to create a depth cue by exploiting the fact that objects appear smaller at a distance, thus even though we are drawing simple 2D shapes, the resulting image appears to have depth.

float w = r/k + AMPLITUDE * sin(theta + PI * PERIOD_MUL / k);

Then we calculate the distance from the shape and fade the value based on a constant, the polar radius and the iteration index. Fading the value reinforces the perception of depth. The resulting value is accumulated for the current pixel.

f += ring(w) * BRIGHTNESS * pow(k,FADE) * r;

The shape is calculated as a simple clamping of distance values based on the offset radius. Note that since we have modified r based on the sine wave above, this calculation is actually not mathematically correct. This a general issue when using distance fields; the distance function is linear, however the domain is non-linear. For the purpose of this experiment this is fine as the shapes we draw are too thin to notice the issue and it allows using a simple estimator.

float ring(float r) { return step(r, RING_MAX) - step(r, RING_MIN); }

Finally, we perform a simple contrast adjustment and set the final value for the pixel.

}
fragColor = vec4(vec3(pow(f,CONTRAST)), 1);

Configurations

The shape you see above is just one of infinite possible configurations. The code allows for heavy parametrization of the geometry. Play around with the values and see what interesting shapes you can make.

Here are a few examples:

#define AMPLITUDE  (0.40)
#define PERIOD     (1.00)
#define PERIOD_MUL (3.00)
#define SCALE      (1.50)
#define RING_MIN   (0.97)
#define RING_MAX   (1.00)
#define FADE       (5.00)
#define BRIGHTNESS (0.25)
#define CONTRAST   (0.85)
#define ITERATIONS (75)

#define AMPLITUDE  (0.30)
#define PERIOD     (2.00)
#define PERIOD_MUL (2.00)
#define SCALE      (1.50)
#define RING_MIN   (0.97)
#define RING_MAX   (1.00)
#define FADE       (3.00)
#define BRIGHTNESS (0.10)
#define CONTRAST   (0.65)
#define ITERATIONS (100)

#define AMPLITUDE  (0.50)
#define PERIOD     (3.00)
#define PERIOD_MUL (2.00)
#define SCALE      (2.00)
#define RING_MIN   (0.95)
#define RING_MAX   (1.00)
#define FADE       (2.00)
#define BRIGHTNESS (0.10)
#define CONTRAST   (1.0)
#define ITERATIONS (100)

References / Further Reading